Acknowledgement

We gratefully acknowledge funding support from :
- National Science Foundation – Division of Materials Research- Condensed Matters and Materials Theory Program – CMMT – DMR-1954621 – 2020-2024
- National Science Foundation – Division of Materials Research – CERAMICS, DMREF – DMR-2119308 – 2021-2025
- Chicago/DOE Alliance Center (CDAC) – DE-NA0004153 – 2024-2028
Computational resources are provided by:
- NSF funded Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS). 2024-present
- UIC’s Electronic Visualization Lab (EVL) funded by NSF Award: CNS-1828265. Our special thanks to Dr. Lance Long for their support. 2020-present
- Extreme Science and Engineering Discovery Environment (XSEDE). 2019-2023
Overview
Throughout the use of quantum mechanical and atomic-scale modeling techniques, combined with theoretical consideration, we investigate the connection between the microscopic physical phenomena and the thermodynamic and kinetic properties in materials. This lab pursues three primary lines of research.
- Integration of first-principles and atomistic simulation tools into cohesive and automated computational frameworks, in order to facilitate or accelerate the thermodynamic and kinetic investigation of certain types of materials.
- Deployment of sophisticated electronic structure and empirical potential simulation tools (e.g. VASP, ABINIT, and LAMMPS) to predict the properties of materials, specially to aid us in in silico discovery of novel materials in a range of applications, such as structural materials, energy storage materials, and ferroelectric materials.
- Development of high-throughput (HT) frameworks by utilizing the emerging tools in data science, such as machine learning and deep learning. These HT frameworks provide us with cost-effective yet accurate tools and aid us in discovery of new materials for different applications.
For an updated list of publications, refer to our Google Scholar page.
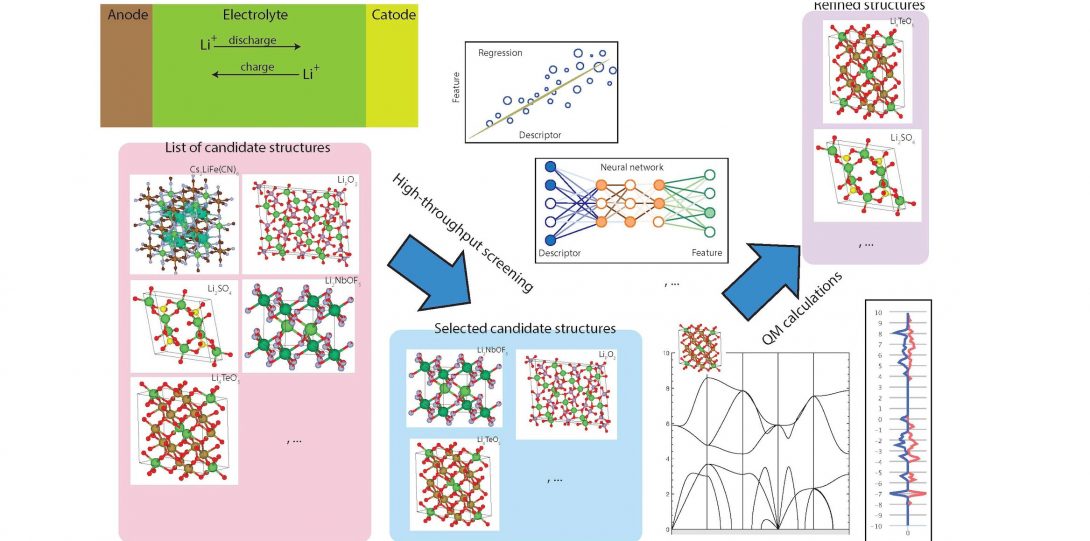
Machine Learning for Materials Discovery and Optimization
Predicting structure-property relation for most materials is often complicated and requires computationally-intensive first-principles calculations. Additionally, some material’s properties or behaviors are inherently dependent on the interplay of many parameters and factors, making their prior prediction even more challenging. For example, predicting whether a certain crystalline form of a compound can be synthesized or naturally formed is not an easy task! This is because the synthesizabiliy of a crystalline material is governed by many parameters, such as thermodynamic stability, the kinetics of the synthesis process, and synthesis routes (synthesis history), making a one-on-one map of synthesizability to simple physical parameters infeasible.
In our lab, we combine sophisticated machine learning algorithms with physical theories and expert knowledge to predict materials properties and provide guidelines to accelerate their discovery and optimization. Our goal is to utilize machine learning methods to develop predictive models that can tackle complicated problems that are yet to be modeled by current theoretical frameworks.
References
- Ali Davariashtiyani, Busheng Wang, Samad Hajinazar, Eva Zurek, Sara Kadkhodaei. Impact of Data Bias on Machine Learning for Crystal Compound Synthesizability Predictions (Machine Learning Science and Technology, Accepted). preprint: https://doi.org/10.48550/arXiv.2406.17956
- Ali Davariashtiyani and Sara Kadkhodaei. Formation energy prediction of crystalline compounds using deep convolutional network learning on voxel image representation. Communications Materials, 4(1): 105, Dec 2023. ISSN 2662-4443. doi: 10.1038/s43246-023-00433-9. URL https://doi.org/10.1038/s43246-023-00433-9
- Ali Davariashtiyani, Zahra Kadkhodaie & Sara Kadkhodaei. (2021). Predicting synthesizability of crystalline materials via deep learning. Communications Materials volume 2, Article number: 115 URL: https://doi.org/10.1038/s43246-021-00219-x
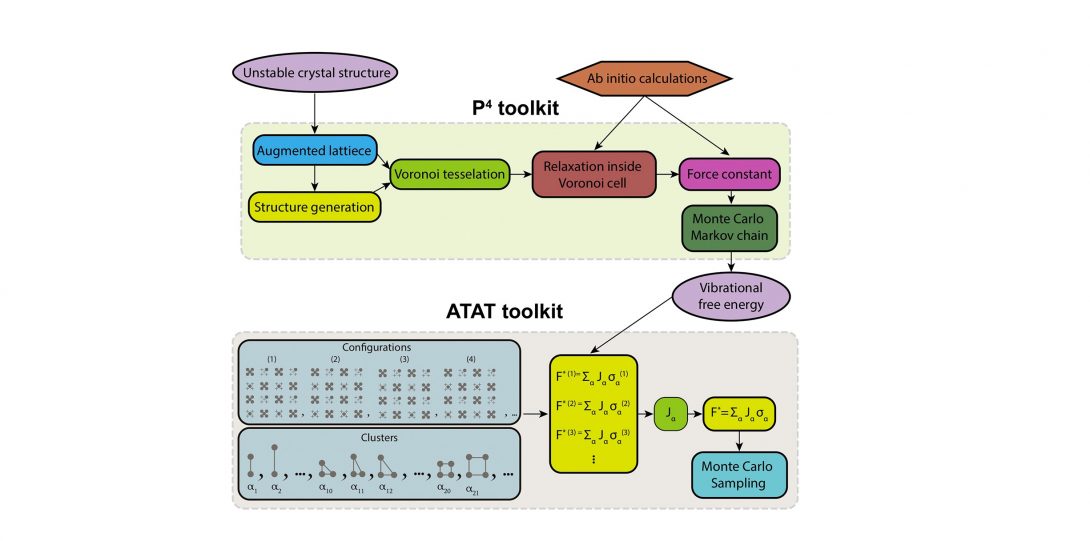
Diffusion phenomena and defects in materials

Diffusion is the underlying mechanism for many materials-related processes and microstructure evolution which in turn determine the stability, physical properties, and mechanical performance of materials. To gain a fundamental understanding of kinetics of precipitation, oxidation, creep, and phase transformation it is essential to be acquainted with fundamentals of diffusion. In our lab, through development of sophisticated computational techniques, we unravel the origins of diffusion-based phenomena in different materials and provide schemes that balance the trade-off between computational efficiency and diffusion prediction accuracy.
References
- Seyyedfaridoddin Fattahpour and Sara Kadkhodaei. Improving ab initio diffusion calculations in materials through Gaussian process regression. Phys. Rev. Materials 8, 013804 (2024) DOI https://doi.org/10.1103/PhysRevMaterials.8.013804
- Seyyedfaridoddin Fattahpour, Ali Davariashtiyani, and Sara Kadkhodaei (2022), Understanding the role of anharmonic phonons in diffusion of bcc metals. Phys. Rev. Materials 6, 023803 DOI https://journals.aps.org/prmaterials/abstract/10.1103/PhysRevMaterials.6.023803
- Kadkhodaei, S. and Davariashtiyani A. (2020). Phonon-assisted diffusion in bcc phase of titanium and zirconium from first principles. Phys. Rev. Materials 4, 043802 DOI https://journals.aps.org/prmaterials/abstract/10.1103/PhysRevMaterials.4.043802
- Kadkhodaei, S. and van de Walle, A. (2019). A simple local expression for the prefactor in transition state theory. The Journal of Chemical Physics, 150(14), p.144105. DOI https://aip.scitation.org/doi/abs/10.1063/1.5086746
Thermodynamics of Defects

Defects in semiconducting compounds regulate charge carrier density and, consequently, the electrical properties, directly impacting the performance of electronic devices such as thermoelectrics, transistors, and solar cells. While traditionally, the Gibbs energy for defective compounds has been developed empirically, we have introduced a theoretical framework that directly connects defect energetics at electronic and atomic levels to a universally parameterized Gibbs energy function in the dilute range. This universal parameterization enables a consistent description of Gibbs energy across varying coexistence conditions, accommodating different chemical potentials and Fermi levels. This formalism for defect energy represents a significant advancement in the first-principles parameterization of the thermodynamics of defective compounds.
References
- Amir M. Orvati Movaffagh, Adetoye Adekoya, Sara Kadkhodaei. Defect energy formalism for CALPHAD thermodynamics of dilute point defects: Theory (Physical Review Materials, Accepted). preprint: https://doi.org/10.48550/arXiv.2407.12301
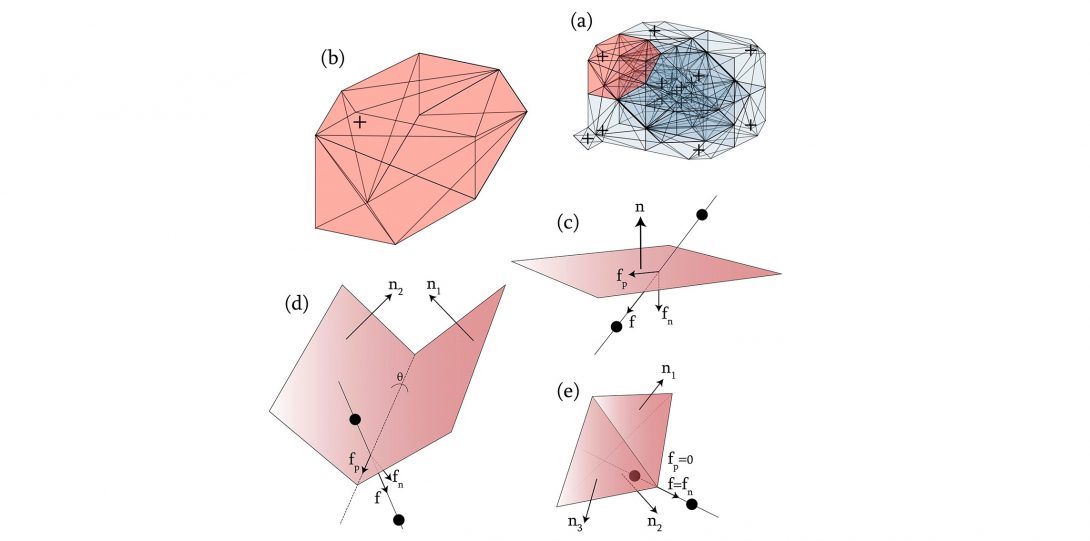
Finite Temperature Effects on Materials Stability
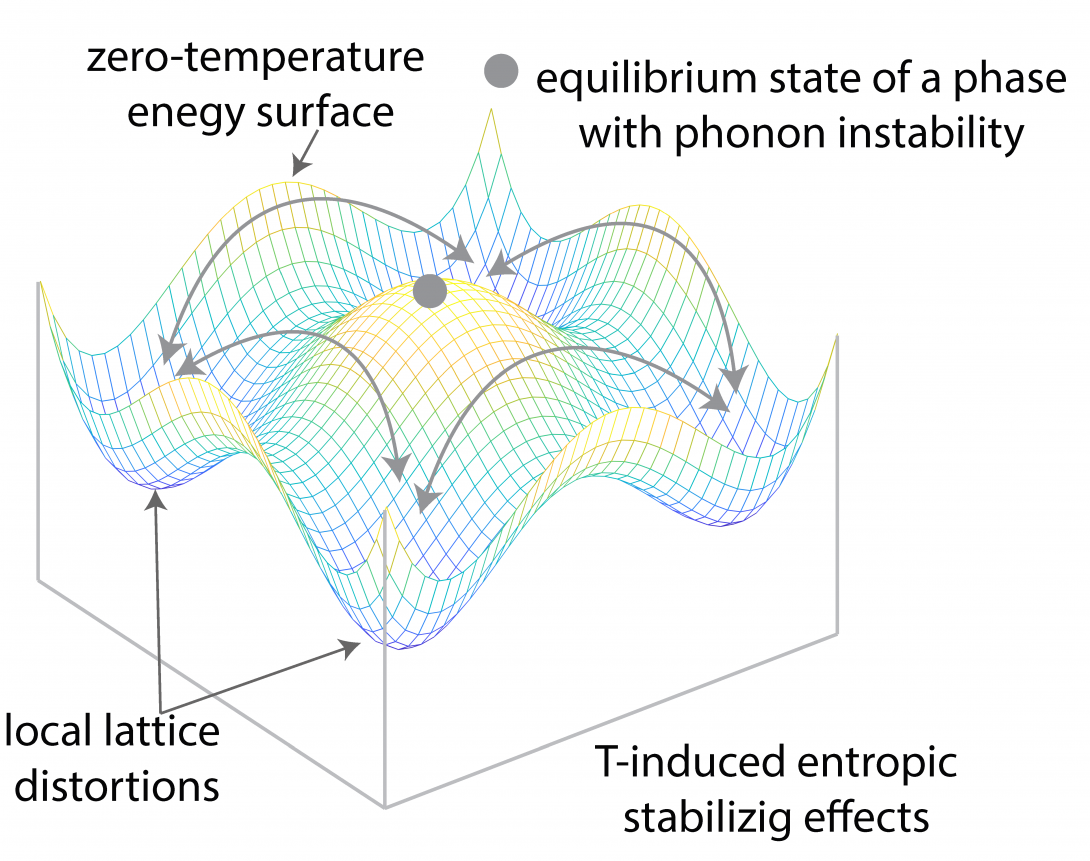
The equilibrium state of matter is governed by the fundamental laws of thermodynamics. The interplay among internal energy and entropy becomes a crucial factor in materials stability at finite temperatures. The concept of entropy is more difficult to comprehend when compared to energy. From the statistical mechanics point of view, entropy is a measure of randomness in microscopic states that correspond to a macroscopic observation. For example, vibrational entropy is a measure of the number of ways the thermal energy can be divided between atoms or the number of ways that atoms can vibrate collectively in the solid. In our lab, we combine sophisticated quantum mechanical calculations with statistical mechanics theories to understand and predict finite temperature entropic effects on stability in different material systems. Our goal is to devise theoretical frameworks that can calculate finite temperature entropic effects by introducing new conceptual models and computational techniques.
References
- Kadkhodaei, S. and van de Walle, A. (2019). Software tools for thermodynamic calculation of mechanically unstable phases from first-principles data. Computer Physics Communications.
- Kadkhodaei, S. and van de Walle, A. (2018). First-principles calculations of thermal properties of the mechanically unstable phases of the PtTi and NiTi shape memory alloys. Acta Materialia, 147, pp.296-303.
- Kadkhodaei, S., Hong, Q. and van de Walle, A. (2017). Free energy calculation of mechanically unstable but dynamically stabilized bcc titanium. Physical Review B, 95(6).
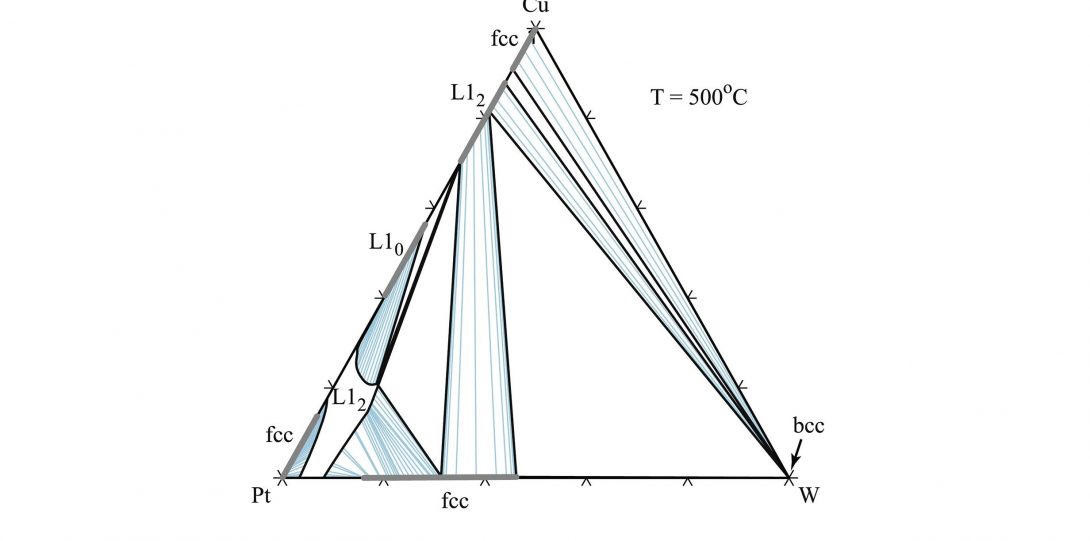
Theory of Alloys
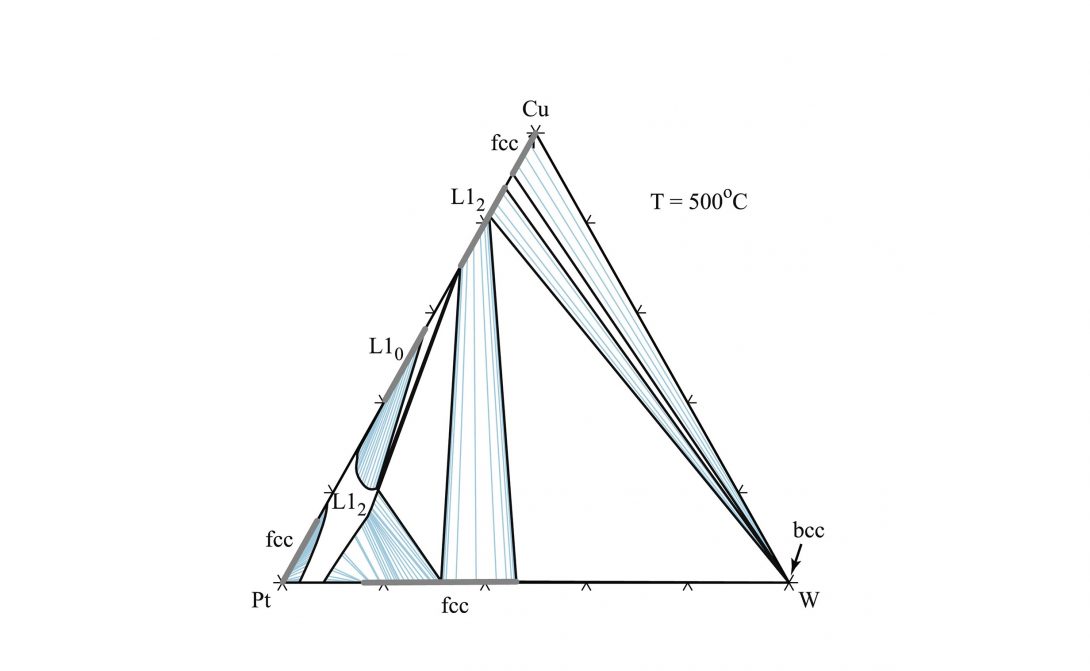
Phase diagrams are roadmaps of phase stability and serve as the basic tool to engineer materials processing. First-principles electronic structure calculation has become an indispensable tool to calculate the phase stability of alloys. However, an important common limitation of many high throughput efforts is their focus on perfectly ordered stoichiometric phases, typically only at absolute zero, while most engineering alloys are nonstoichiometric, feature point defects (often in nondilute amounts) and are processed or used at high temperatures. In our lab, through development of sophisticated computational techniques, we provide simple pathways to overcome this limitation. Our goal is to devise frameworks that balance the trade-off between computational efficiency and phase diagram prediction accuracy to provide useful high-throughput tools for building phase diagrams.
References
- Noel Siony, Long Vuong, Otgonsuren Lundaajamts, Sara Kadkhodaei. (2022) Computational design of corrosion-resistant and wear-resistant titanium alloys for orthopedic implants. Materials Today Communications, Volume 33,104465
- Sara Kadkhodaei & Jorge A. Muñoz. (2021) Cluster Expansion of Alloy Theory: A Review of Historical Development and Modern Innovations. JOM volume 73, pages3326–3346
- van de Walle, A., Kadkhodaei, S., Sun, R. and Hong, Q. (2017). Epicycle method for elasticity limit calculations. Physical Review B, 95(14).
- van de Walle, A., Sun, R., Hong, Q. and Kadkhodaei, S. (2017). Software tools for high-throughput CALPHAD from first-principles data. Calphad, 58, pp.70-81.
- van de Walle, A., Hong, Q., Kadkhodaei, S. and Sun, R. (2015). The free energy of mechanically unstable phases. Nature Communications, 6(1).